11. sınıf öğrencimiz İdil Büyükgölcigezli hazırlamış olduğu matematik TÜBİTAK projesi ile bölge finallerinde birinci olmuş olup aşağıdaki anlattığı projesi ile Türkiye finallerine katılma hakkı kazanmıştır.
Toplam n2 birim kareden oluşan n çarpı n’lik bir karesel düzlem hayal edelim. Bu düzlemin sol alt köşesinden sağ üst köşesine kaç farklı şekilde gidebiliriz? İçinizden bu sorunun ne kadar kolay olduğunu düşündüğünüze eminim. Bu nedenle soruyu biraz zorlaştıralım. Başlangıç noktamız ve hedef noktasını birleştiren bir çapraz çizgi çizelim. İşte bu çizgi, aşağıdaki resimde de turuncu ile gösterilen y=x doğrusu. Başlangıç noktasından hedef noktasına hiç bu doğrunun üzerine çıkmadan kaç farklı şekilde gidebiliriz? Unutmayın takip edeceğiniz yolun bütün noktaları y=x doğrusu ile çakışık olmalı veya onun altında kalmalı. İşte bu sorunun cevabı adını Belçikalı matematikçi Charles Catalan’dan alan Katalan sayıları dizisinin n’inci terimi verir. İlk on Katalan sayısı şöyledir:
1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796
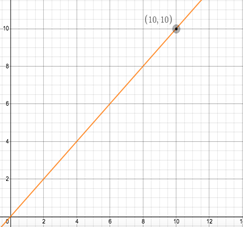
Şekil 1. y=x doğrusu ve (10,10) noktası
Az önce Katalan sayı dizisinin tamamen iki boyutlu düzlemde kalan bir ispatını yapmış olduk. Günlük hayatımızda ise neredeyse her zaman üç boyutlu nesneler ve kavramlarla ilgileniyoruz. Bu nedenle ben de “Karesel bir düzlem yerine bir küpün alt sol köşesinden çaprazındaki üst sağ köşesine x≥y ≥z şartını sağlayarak kaç farklı şekilde gidebiliriz?” sorusunun cevabını merak ettim ve bu sorudan yola çıkarak bir proje hazırladım. Önce yaptığım küp modelleri ile yeni bir Üç Boyutlu Katalan Sayıları Dizisi’ni elde ettim, sonra da bu diziyi ve Katalan Sayıları dizisini kullanarak bir küp üzerindeki hareket problemlerini çözdüm. Bu çözümüm esnasında da bir küpte x≥y ≥z şartını sağlayan nokta sayısının da Dörtyüzlüsel Sayılar ile ilişkili olduğunu ortaya koyarak Katalan Sayıları ve Dörtyüzlüsel Sayılar arasında bir bağ kurdum.
